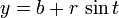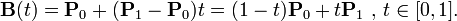Menudas curvas! Tranquilo, porqué no, no es lo que piensas… En este artículo completaré los anteriores que he ido escribiendo, en cuanto a parametrización de trayectorias se refiere (hemos visto ya el círculo, parábola, y curva bézier entre otros tipos de trayectorias). Lo importante aquí es la idea geométrica del asunto (más que si se implementa con XNA o cualquier otra cosa), al final el código siempre será muy parecido a este, sea cual sea el lenguaje de programación. Aquí podéis descargar el código con todos los ejemplos.
Parametrización de una Elipse
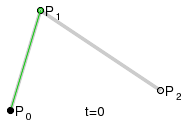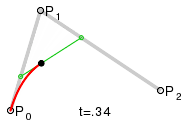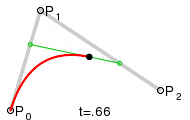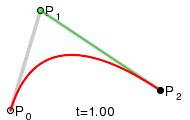
La elipse puede parametrizarse de la siguiente forma:
Considerando que nuestra elipse tiene el punto C como centro, entonces la parametrización se define de la siguiente forma:
Implementar esto en XNA ya es coser y cantar… (sólo habría que considerar, que aquí Y+ sería Y-, ya que las coordenadas se comienzan a contar a partir de la parte superior izquierda de la pantalla a la parte inferior derecha de la misma, es decir, en la parte inferior la Y es positiva, y más arriba de la pantalla, sería positiva). Necesitamos declarar las siguientes variables:
public
Texture2D textura;
public
Vector2 posicion;
public
Vector2 posicionInicial;
public
Vector2 dimensionesElipse;
float
t;
La textura contiene el sprite que pintaremos por pantalla, la posición el punto de la pantalla sobre el cual pintaremos en cada momento el sprite. posicionInicial contiene el centro de la elipse, y dimensionesElipse contiene el ancho y alto de la misma. Finalmente t contendrá una unidad de tiempo, que iremos incrementando para parametrizar la elipse.
A continuación, inicializamos estas variables:
// Situamos el vector posición inicial en mitad de la pantalla
this.posicionInicial
= new Vector2(this.graphics.GraphicsDevice.Viewport.Width / 2, this.graphics.GraphicsDevice.Viewport.Height / 2);
this.posicion
= new Vector2();
// Establecemos dimensiones (ancho y alto) de la elipse
this.dimensionesElipse
= new Vector2(300,
150);
// Iniciamos el tiempo
this.t
= 0.0f;
Cargamos el sprite que vamos a pintar por pantalla:
textura
= this.Content.Load<Texture2D>(«bola»);
Y esta es la parte chula, en el método Update, donde parametrizamos la elipse de sobre el vector posición, a partir de las funciones wikipedianas que hemos visto anteriormente:
// Parametrización de la elipse
this.posicion.X
= this.posicionInicial.X + this.dimensionesElipse.X * (float)Math.Cos(t);
this.posicion.Y
= this.posicionInicial.Y + this.dimensionesElipse.Y * (float)Math.Sin(t);
t
+= 0.015f;
Finalmente, en elm método draw nos limitamos a pintar el sprite en la posición calculada:
this.spriteBatch.Draw(this.textura, this.posicion,
Color.White);
Parametrización de la Espiral de Arquímedes
Para parametrizar una espiral, lo haremos a partir de:
Vamos, que vista la elipse, esto no es mucho más complicado. En la lista de variables ahora tenemos el angulo polar respecto el punto P(x,y):
public
Texture2D textura;
public
Vector2 posicion;
public
Vector2 posicionInicial;
public
float anguloPolar;
En el método update parametrizar la espiral nos va a resultar de lo más fácil:
// Parametrización de la espiral
this.posicion.X
= this.posicionInicial.X + this.anguloPolar * t * (float)Math.Cos(t);
this.posicion.Y
= this.posicionInicial.Y + this.anguloPolar * t * (float)Math.Sin(t);
t
+= 0.015f;
Parametrización del Cardioide
¿Qué es un Cardioide? Tendrás que seguir leyendo para verlo, porqué no pienso poner ningún dibujo. Quizá los más astutos puedan hacerse una idea con sólo ver la parametrización:
Si no has intuido la forma no pasa nada… pocos son los mortales que la conocen. El código, viendo la parametrización, no es muy distinto del anterior:
this.posicion.X
= this.posicionInicial.X + this.anguloPolar * (1 + (float)Math.Cos(t)) * (float)Math.Cos(t);
this.posicion.Y
= this.posicionInicial.Y + this.anguloPolar * (1 + (float)Math.Cos(t)) * (float)Math.Sin(t);
Y e aquí el cardioide:
Parametrización de una Rodonea
Si la curva anterior te ha parecido rara… no se que pensarás cuando veas esta. Una rodonea se parametriza del siguiente modo:
Una vez implementado, obtendremos la curva más rara nunca vista:
Dicho código sería el siguiente:
this.posicion.X
= this.posicionInicial.X + this.anguloPolar * (float)Math.Cos(this.petalos
* t) * (float)Math.Cos(t);
this.posicion.Y
= this.posicionInicial.Y + this.anguloPolar * (float)Math.Cos(this.petalos
* t) * (float)Math.Sin(t);
Y por hoy creo que ya tenemos bastantes curvas… os dejo un adjunto este fichero RAR que contiene distintas soluciones XNA con la implementación de cada una de las curvas.