En un videojuego nos puede interesar que los sprites (2D) o Modelos (3D) se muevan en trayectorias no lineales… Esto dará a nuestras animaciones más «naturalidad» y por consiguiente realismo. Si repasamos un poco de geometría y física de cuando eramos unos chavales podremos conseguir algunas trayectorias interesantes sin demasiado esfuerzo. Los ejemplos están realizados con XNA… la idea básica evidentemente es válida para cualquier plataforma de desarrollo.
Parametrización de una circunferencia (trayectoria circular)
Podemos encontrar cualquier punto de una circunferencia con radio r, con centro en el punto (x, y) tiene las coordenadas: P = (r•cos(angulo) + x0, r•sin(angulo) + y0). Esto se ha obtenido a partir de la siguiente expresión, obtenida a partir del Teorema de Pitágoras (sin entrar en mucho más detalle en el concepto matemático):
Es decir, que para trazar una trayectoria circular de cualquier objeto, podremos utilizar simplemente el siguiente código en el método Update de nuestro Game en XNA:
// (x,y) = (r•cos(angulo) + x0, r•sin(angulo) + y0)
float r = 100;
if (angulo == 360)
angulo = 0;
else
angulo+=0.05f;
posicion = new Vector2(r * (float)Math.Cos(angulo) + posicionInicial.X, r * (float)Math.Sin(angulo) + posicionInicial.Y);
Donde la variable posicion es un Vector2 (la posición en cada momento del juego del elemento formando una trayectoria circular), y la variable posicionInicial es el centro del círculo (también de tipo Vector2). Tenéis el código completo disponible en el fichero adjunto Trayectoria_Circular.rar, que lo que hace es mover un sprite trazando precisamente una trayectoria circular.
Por el mismo precio, dejo otra versión del código que además de mover un sprite simple, lo va rotando a medida que va siguiendo la trayectoria de la circunferencia. Esto es muy útil, en nuestro caso hemos puesto un bitmap que es un coche visto desde arriba, dando la sensación de que este está moviéndose pero girando su dirección (no simplemente dando vueltas orientado siempre en la misma dirección). Para ello rotaremos el bitmap en el mismo ángulo en cada momento en que estemos obteniendo la posición, así tendremos un bitmap en ángulo recto respecto este ángulo (esto se ve mejor con un dibujo):
Esto lo haremos con el código siguiente:
spriteBatch.Draw(this.sprite, this.posicion, null, Color.White, angulo, new Vector2(this.sprite.Width / 2, this.sprite.Height / 2), 1.0f, SpriteEffects.None, 0f);
En el adjunto Trayectoria_Circular_RotacionSprite.rar he dejado el ejemplo completo, en el que se ve un coche dando vueltas de forma circular, hasta el infinito…
Trayectoria de un proyectil
Esto es física de hace ya años… aunque reconozco que he tenido que rascarme la cabeza para volver a encontrar las fórmulas para parametrizar la trayectoria de un proyectil 😛
Se consigue con la fórmula siguiente:
x = v0 • cos(angulo) • t
y = v0 • sin(angulo) • t – (1/2) • g • t^2
Observad que no se ha considerado ninguna fricción con el aire, por lo que la velocidad en el eje X sería constante. Esto, en código, viene a suponer lo siguiente:
this.posicion.X = this.posicionInicial.X + v0 * (float)Math.Cos(angulo) * t;
this.posicion.Y = this.posicionInicial.Y + v0 * (float)Math.Sin(angulo) * t – (float)(.5 * g * (t * t));
Esto teniendo en cuenta que hemos declarado las siguientes constantes generales:
const float v0 = 50.0f;
const float angulo = 80.0f;
const float g = -4.0f;
Velocidad inicial, el ángulo del disparo y la gravedad. Si ejecutamos el código Trayectoria_DisparoParabolico.rar veremos el movimiento aproximadamente parabólico del proyectil.
Trayectoria de una curva lineal Bézier
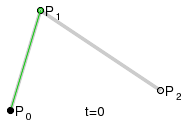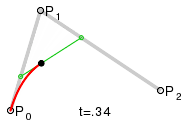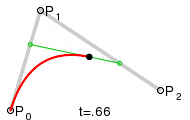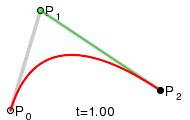
Esta quizá sea la más interesante. La idea de una curva Bézier no es compleja. Conocida la posición de dos puntos (a los que se les llama nodos), definiremos unos puntos «invisibles» llamados puntos de control. Dicho esto el Sr. Pierre Bézier definió una expresión matemática para definir esta curva ya en 1960 (que bonita es la historia).
Función de una curva lineal (no se porqué se le llama curva si acaba dibujando una recta, pero bueno…):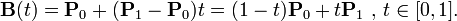
Función de una curva cuadrática. Esta es la que nos interesa. Dibuja una curva entre dos nodos mediante dos puntos de control. Se obtiene mediante la función:
Este dibujo ilustra la curva bézier cuadrática (como me gusta el nombre jeje):
La expresión que ya hemos visto se traduce del siguiente modo en XNA:
this.posicion = (float)Math.Pow((1 – t), 2) * pos0 + 2*t*(1-t) * pos1 + (float)Math.Pow(t, 2) * pos2;
t += 0.005f;
¿Fácil? 😛 Nuestro amigo Pierre era un crack, todo hay que decirlo. Ala, aquí os dejo el código por si queréis ejecutarlo y ver como queda: Trayectoria_Beizer.rar
Nota: Varias de las imágenes y fórmulas han sido obtenidas de la Wikipedia
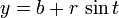
Buen refresco y recopilatorio… perfecto!
Gracias!
La interpolación lineal es un método sencillo para describir trayectorias entre distintos
This is a great tutorial! It helped me out with some trouble I’ve been having on a game I am developing where you point the mouse on the screen and missiles are shot based of a rotated object on screen that is magnetic to the position of the mouse. The object rotates based on the mouse position. I figured out the math myself but I didn’t add on the radians at the end!
I had to translate this to English using Google Translate! You should consider multi-lingual text for your website, alot of American developers would like the info on your site!
Thanks a lot… I’ll think about your suggestion
hola, tu tutorial esta muy completo, pero a mi me surgue un problema, manejo a mis enemigos con una lista, y aparte del m ovimiento circular, tengo la intenicon de hacer que avanzen hacia la izquierda, (x–), el punto es que entre mas enemigos hay en pantalla, mi radio se hace mas pequeño(o es lo que entiendo), llega el momento donde ya solo se ven «vibrar»