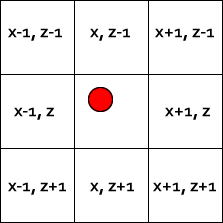
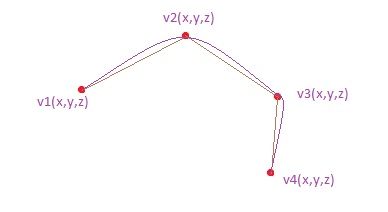
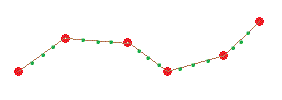
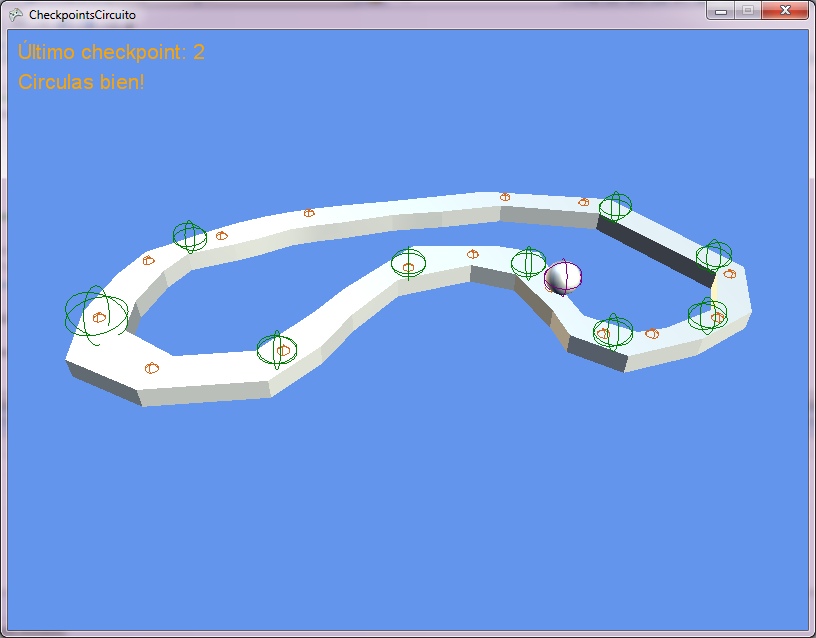
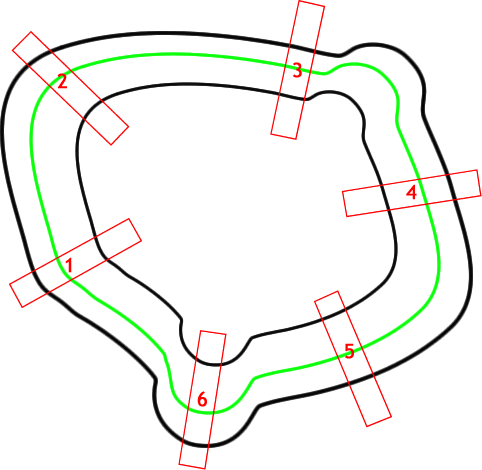
¿Cómo funcionan los juegos de carreras? De una forma muy compleja xD La pregunta más bien debería ser: ¿Cómo validamos que los coches recorren el circuito sin hacer trampas? Posible respuesta: mediante un sistema de checkpoints. Es decir, cada cierta distancia, validar que el vehículo del jugador está avanzando en la dirección correcta, y que además no se ha salido de la carretera para tomar atajos «excesivos». Con atajos, me refiero (ver la imagen de debajo), a que el jugador no vaya del punto 1 al 4 por el centro del circuito y gane la carrera pasándose de listillo… este sistema de checkpoints también puede ser útil para indicarle al jugador si va en dirección contraria.
Implementación
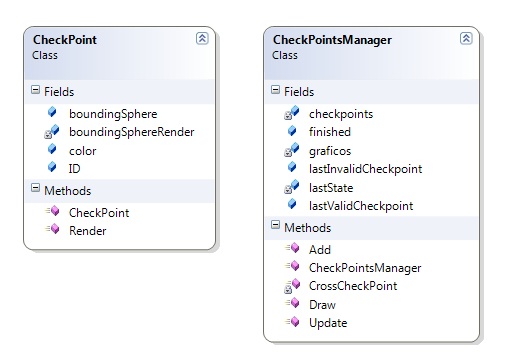
Vamos a centrarnos únicamente en el sistema de checkpoints (quitando por unos momentos importancia a renders, cámaras, etc). Dicho esto, el código resulta bastante sencillo. Tendremos dos clases: CheckPoint y CheckPointsManager. Un CheckPoint no es más que un boundingSphere y un ID (para distinguir unos checkpoints de otros y tenerlos ordenados). Contiene además un método de renderizado, que utilizaremos para «pintar» los checkpoints en pantalla -esto sólo tiene sentido si estamos debugando, ya que durante la ejecución del juego los checkpoints deberían ser «invisibles» para el jugador-.
El CheckPointsManager contiene todos los CheckPoint de un circuito (en el atributo List<Checkpoint> checkpoints). Además indica si hemos completado el circuito (bool finished), así como información de uso interno para la lógica de la clase, como por ejemplo cuál ha sido el último checkpoint válido o incorrecto que hemos atravesado.
¿Cómo utilizamos estas clases? Lo primero será, en la clase Game (clase principal del juego) inicializar la clase CheckpointsManager, e irle añadiendo checkpoints. Esto es tan fácil como…:
checkPointsManager = new CheckPointsManager(GraphicsDevice);
CheckPoint check1 = new CheckPoint(new Vector3(0, -100, 300), 100);
CheckPoint check2 = new CheckPoint(new Vector3(400, -100, 200), 100);
CheckPoint check3 = new CheckPoint(new Vector3(700, -100, -300), 100);
CheckPoint check4 = new CheckPoint(new Vector3(400, -100, -1000), 100);
CheckPoint check5 = new CheckPoint(new Vector3(0, -100, -1200), 100);
CheckPoint check6 = new CheckPoint(new Vector3(-400, -100, -1000), 100);
CheckPoint check7 = new CheckPoint(new Vector3(-700, -100, -300), 100);
CheckPoint check8 = new CheckPoint(new Vector3(-400, -100, 200), 100);
checkPointsManager.Add(check1);
checkPointsManager.Add(check2);
checkPointsManager.Add(check3);
checkPointsManager.Add(check4);
checkPointsManager.Add(check5);
checkPointsManager.Add(check6);
checkPointsManager.Add(check7);
checkPointsManager.Add(check8);
Como se puede observar, un checkpoint tiene un vector de posición 3D (X, Y, Z), y un valor numérico, que es el radio del checkpoint (el espacio físico que ocupará el boundingbox). Con esto tenemos el CheckPointsManager inicializado… Este código de inicialización lo pondríamos en el método Initialize de la clase Game (¿evidente, no?)
Con esto tenemos los checkpoints del circuito… pero nos falta lo más importante, el agente que el jugador va a desplazar entre los checkpoints. Y además también añadiremos un sencillo circuito, para que se vea más claro el desplazamiento de los objetos en pantalla. Fácil, fácil, en la clase principal del juego (Game), declaramos estos objetos:
ExtendedModel agente;
ExtendedModel circuito;
Después sólo nos queda inicializar ambos…
// Iniciamos el agente
agente = new ExtendedModel();
agente.position = new Vector3(0.0f, 0.0f, 300.0f);
agente.scale = 10.0f;
agente.fAlt_Avatar = 80.0f;
agente.fAmple_Avatar = 80.0f;
// Inicializamos el circuito
circuito = new ExtendedModel();
circuito.scale = 10.0f;
circuito.position = new Vector3(0, -300, -500) ;
circuito.rotation = new Vector3(MathHelper.ToRadians(-90), 0, 0);
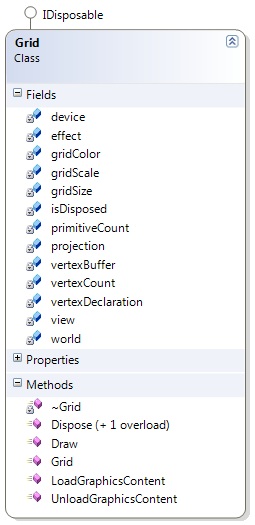
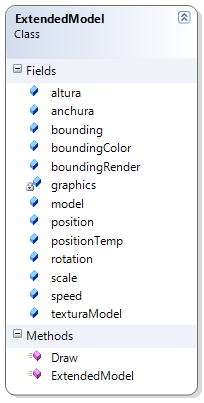
Un momento… ¿que es el objeto ExtendedModel? Es una clase personalizada que contiene un objeto de tipo modelo, así como información adicional que nos es de interés como la posición, escala y rotación. Es una forma de simplificar el posicionamiento y rotación de los modelos. La definición completa de la clase es la siguiente:
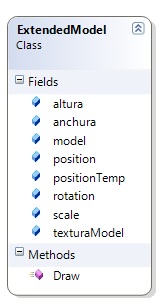
Una vez inicializados estos objetos, habrá que cargar los modelos de cada uno de ellos en el método LoadContent de la clase Game. Trivial:
circuito.model = Content.Load<Model>(@»Modelscircuito»);
agente.model = Content.Load<Model>(@»Modelsbola»);
Para los más profanos de XNA, comentar que estos modelos han sido diseñados y exportados con 3DMAX 2009, y grabados al formato FBX (que junto al formato X, son los formatos de modelos que por defecto «entiende» el Content Pipeline de XNA). Aunque cuando podáis ver como son los modelos en este ejemplo (una simple esfera y una variación de toroide), veréis que no es necesario ser un gran diseñador 3D ni dominar MAX para modelar nuestras pequeñas pruebas como programadores.
Ahora lo interesante es que el agente se desplace por la pantalla con los movimientos del cursor de teclado.. (o más específicamente, con las letras A/S/D/W/X). Para ello, introduciremos el siguiente código en el método Update() de la clase Game.
KeyboardState kbState = Keyboard.GetState();
if (kbState.IsKeyDown(Keys.A))
{
agente.position.X -= 4.0f;
}
if (kbState.IsKeyDown(Keys.D))
{
agente.position.X += 4.0f;
}
if (kbState.IsKeyDown(Keys.W))
{
agente.position.Z -= 4.0f;
}
if (kbState.IsKeyDown(Keys.S))
{
agente.position.Z += 4.0f;
}
Se diría que hasta aquí todo es «normal», hace rato que no hablamos de los checkpoints… pues volvamos a ellos. La clase CheckPointsManager tiene un método Update(). Este método refresca la lógica de los checkpoints, y es la que indica si nuestro agente se está desplazando correctamente o no… (este código habrá que ejecutarlo desde el método también llamado Update de la clase Game):
this.checkPointsManager.Update(this.bounding);
¿Qué es el parámetro bounding que acepta el método update? Es un BoundingSphere, utilizado para la detección de colisiones entre el agente y los checkpoints. Los boundingBox y boundingSpheres son muy utilizados para la detección de colisiones en 3D, dan para varios artículos ellos solos… muy resumidamente, los BoundingBoxes y BoundingSpheres son objetos que el jugador no ve, que engloban algo cuyas colisiones queramos detectar (por ejemplo un checkpoint y el jugador). Entonces es muy fácil detectar si hay colisión entre dos BoundingSpheres o BoundingBox, ya que estas clases tienen un método Intersects, que aceptan otro objeto del mismo tipo como parámetro. Una imagen vale más que mil palabras:
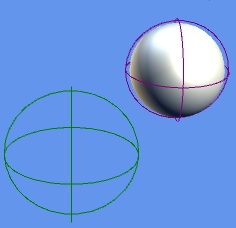
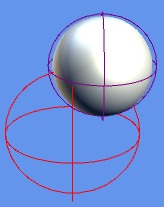
La primera imagen muestra dos boundingSpheres sin colisión (una de ellas «encapsula» a nuestro agente), y la segunda muestra los mismos boundingsphere con colisión (hemos desplazado el agente, y su boundingsphere con él).
Volviendo al tema que nos ocupa… los checkpoints. La llamada al método Update de la clase CheckpointsManager devolverá un valor bool, que nos permetirá saber si el jugador se mueve en dirección adversa o reversa. Aquí podremos hacer con esta información lo que queramos (una opción sería descalificar al jugador si va en sentido contrario). En nuestro caso mostramos unos mensajes por pantalla dependiendo de este resultado:
// Control de los checkpoints
bool vamosBien;
vamosBien = this.checkPointsManager.Update(this.bounding);
if (!this.checkPointsManager.finished)
if (vamosBien)
mensajePantalla = «Circulas bien!»;
else
mensajePantalla = «Circulas en dirección contraria!!!»;
else
mensajePantalla = «Eres el amo, has completado el circuito!»;
Ya solo nos queda dibujar todo esto por pantalla… esto lo haremos colocando el código siguiente en el método Draw() de la clase Game.
GraphicsDevice.Clear(Color.CornflowerBlue);
agente.Draw(view, projection);
checkPointsManager.Draw(view, projection);
circuito.Draw(view, projection);
boundingRender.Render(bounding, GraphicsDevice, view, projection, Color.Purple);
base.Draw(gameTime);
spriteBatch.Begin(SpriteBlendMode.AlphaBlend, SpriteSortMode.FrontToBack, SaveStateMode.SaveState);
int ultimoCheckpoint = 0;
if (checkPointsManager.lastValidCheckpoint != null)
ultimoCheckpoint = checkPointsManager.lastValidCheckpoint.ID;
spriteBatch.DrawString(this.fuente, «Último checkpoint: « + ultimoCheckpoint.ToString(), new Vector2(10, 10), Color.Orange);
spriteBatch.DrawString(this.fuente, mensajePantalla, new Vector2(10, 40), Color.Orange);
spriteBatch.End();
Esta clase de CheckPointsManager viene a ser pues nuestra «caja negra» de los checkpoints. Podemos añadirle cuantos checkpoints queramos, y olvidarnos de la gestión de los mismos, pues esta clase se encargará de ello.
El resultado final es el siguiente http://www.youtube.com/watch?v=96tuLF6CCW4:
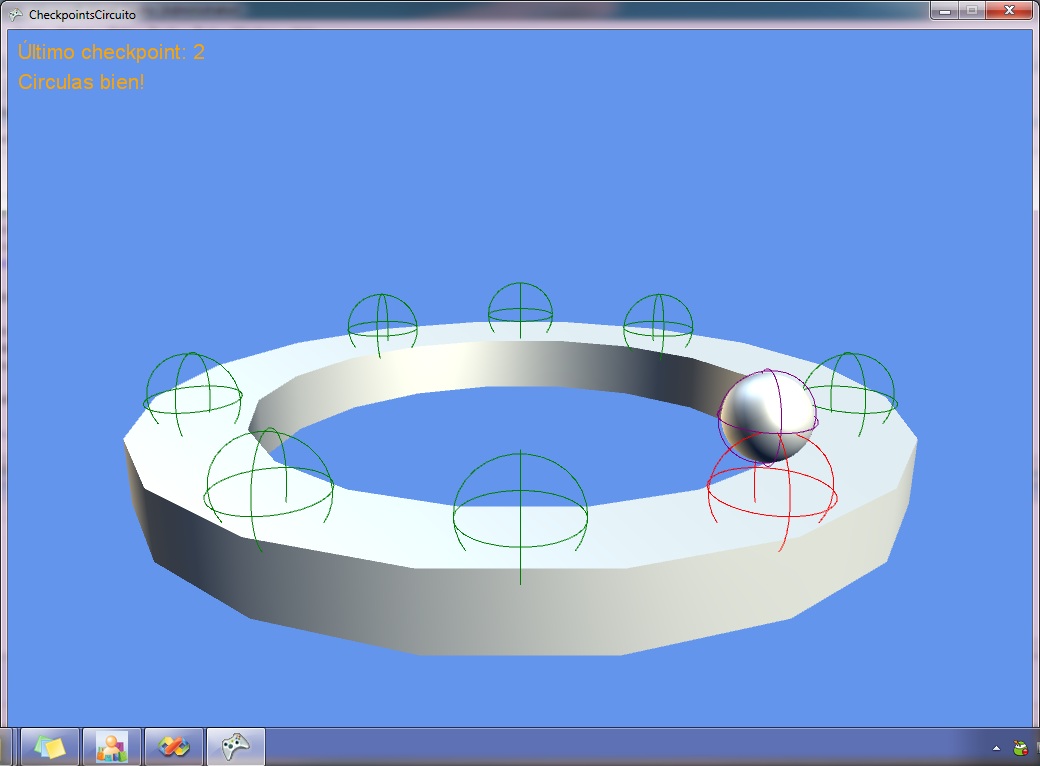
El código se puede descargar mediante este enlace.