La interpolación lineal es un método sencillo para describir trayectorias entre distintos puntos, usando polinomios lineales. Esto, aplicado a la programación gráfica, significa que nos será muy útil para trazar trayectorias a objetos, cámaras o luces de modo práctico y rápido.
[View:http://www.youtube.com/watch?v=TejebjO-8ts:550:0]
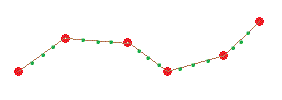
Para describir las «curvas» se utiliza la definición de unos pocos puntos, a los que llamaremos keyframes. Entre ellos, mediante la técnica matemática de los splines, realizaremos la interpolación. El siguiente dibujo ilustra más lo explicado:
En el dibujo, los puntos rojos representan los keyframes, entre ellos, realizaremos una interpolación lineal que nos dará la posición de los puntos verdes, lo cual resultará finalmente en el trazado de la trayectoria que estamos buscando.
Cómo se calcula la interpolación lineal entre dos puntos conocidos
La interpolación lineal consiste en trazar una recta que pasa por (x1,y1) y (x2,y2), y = r(x) y calcular los valores intermedios según esta recta en lugar de la función y = f(x)
Saltándonos un poco el proceso matemático (esto se puede consultar directamente en la wikipedia), tenemos que:
Lo mejor de todo es que XNA ya tiene una función propia para interpolar, llamada Lerp (método estático dentro de la clase Vector3). Eso sí, siempre es bueno saber de dónde vienen los números… ahí queda la fórmula pues.
Cómo aplicaremos estos cálculos a nuestro videojuego
Si recoráis en el «episodio anterior» (siempre quise decir eso) vimos como definir un sistema de checkpoints sobre un circuito. Lo que ahora haremos, pues, va a ser mover el agente que utilizamos en ese ejemplo a través del circuito, de forma «autónoma», de forma que atraviese todos los checkpoints. Esto lo haremos, por supuesto, ¡mediante la trayectoria descrita en la interpolación lineal! (y es que no hay nada más bonito que ver la aplicación real de las matemáticas).
Lo que pasa, es que como somos muy valientes, vamos a complicar un poco más el circuito, para que se vea claramente que no hay «trampa». El anterior circuito era circular, y en un circuito así no haría falta complicarnos la vida con las interpolaciones… nos bataría con la parametrización de una circunferencia. Pero la vida no acostumbra a ser tan sencilla como lo es una circunferencia, y no conozco ningún circuito que sea tan simple. Así que utilizaremos un circuito más complicado, como ya he dicho.
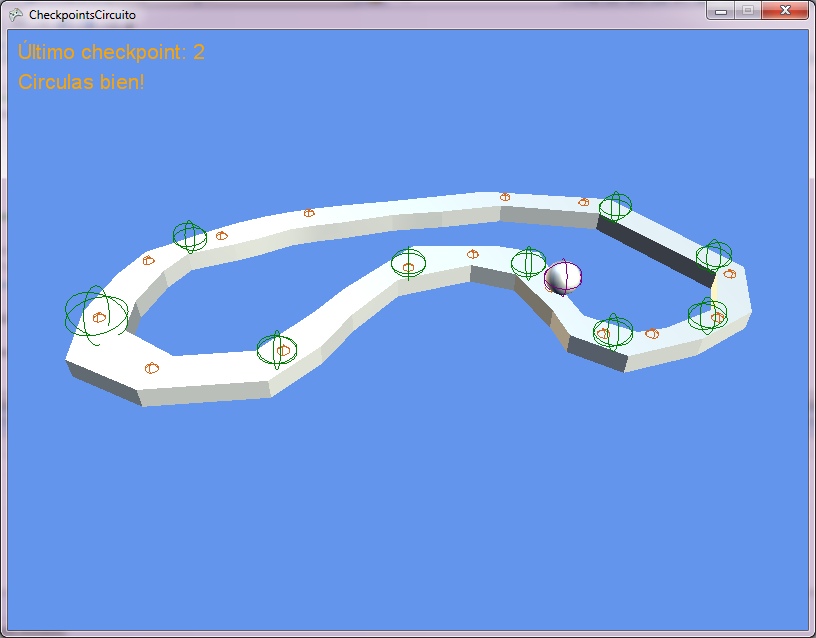
Para ello, lo primero que haremos será abrir el proyecto anterior (el código está definido y explicado en el ejemplo de los checkpoints, que ya he mencionado), y definiremos nuevos checkpoints para el nuevo circuito (así es como se ve renderizado desde 3DMax):
Definiremos los checkpoints del siguiente modo:
checkPointsManager = new CheckPointsManager();
CheckPoint check1 = new CheckPoint(new Vector3(0, -100, -550), 75);
CheckPoint check2 = new CheckPoint(new Vector3(525, -100, -550), 75);
CheckPoint check3 = new CheckPoint(new Vector3(800, -100, -100), 75);
CheckPoint check4 = new CheckPoint(new Vector3(1200, -100, -200), 75);
CheckPoint check5 = new CheckPoint(new Vector3(1350, -100, -600), 75);
CheckPoint check6 = new CheckPoint(new Vector3(1000, -100, -1000), 75);
CheckPoint check7 = new CheckPoint(new Vector3(-1000, -100, -750), 75);
CheckPoint check8 = new CheckPoint(new Vector3(-1250, -100, -200), 120);
CheckPoint check9 = new CheckPoint(new Vector3(-500, -100, 0), 75);
checkPointsManager.Add(check1);
checkPointsManager.Add(check2);
checkPointsManager.Add(check3);
checkPointsManager.Add(check4);
checkPointsManager.Add(check5);
checkPointsManager.Add(check6);
checkPointsManager.Add(check7);
checkPointsManager.Add(check8);
checkPointsManager.Add(check9);
Esto situará algunos checkpoint en el circuito.
Diseño de un sistema que calcule las interpolaciones lineales entre los keyframes
Ahora debemos pensar en un diseño que nos permita almacenar los Keyframes y la interpolación entre los mismos. Yo os propongo un SplinesManager, cuya estructura es muy similar al checkPointsManager:
No acostumbro a usar las clases anidadas, pero en este caso me lo he permitido, ya que la clase Spline sólo la usará el SplinesManager. Por cierto… esta interpolación lineal nada tendría que ver con los splines… pero lo dejo así para el próximo artículo-tutorial, en que se verá otro tipo de interpolación más sofisticada.
De esta clase destacan en importancia la lista de keyframes:
/// <summary>
/// Keyframes principales de la trayectoria
/// </summary>
List<Spline> keyFrames;
/// <summary>
/// Posición intermedia a cada keyframe
/// </summary>
List<Spline> detailedInterpolation;
Los comentarios son bastante aclarativos. La primera lista contiene los keyframes que introducirá el programador. La segunda lista es más detallada, contendrá la interpolación detallada entre todos estos keyframes. Desde la clase Game definiremos nuestros keyframes (en el código adjunto existen más keyframes, pongo sólo estos por brevedad):
SplinesManager.Spline spline1 = new SplinesManager.Spline(new Vector3(0, -200, -650));
SplinesManager.Spline spline2 = new SplinesManager.Spline(new Vector3(300, -200, -750));
splinesManager.AddKeyframe(spline1);
splinesManager.AddKeyframe(spline2);
¿Cómo calculamos la interpolación lineal entre estos keyframes?
En el principio del artículo hemos visto que existe un modo matemático de obtener la información. En XNA, Microsoft nos ha simplificado la vida con la función Vector3.Lerp de la que ha he hablado. El método GenerarInterpolacion() se llamará una vez se hayan añadido todos los keyframes (y sólo se ejecutará una vez). Generará la interpolación detallada con el nivel de detalle especificado en la variable steps. En este caso le he dado un valor de 100. Esto quiere decir que entre keyframe y keyframe habrá 100 posiciones definidas. En este caso el nivel de detalle es alto… podría ajustarse dependiendo del tipo de juego y la velocidad a la que queremos que se muevan los objetos.
/// <summary>
/// Genera interpolación detallada entre los keyframes
/// </summary>
public void GenerarInterpolacion()
{
detailedInterpolation.Clear();
for (int i = 0; i < keyFrames.Count-1; i++)
{
for (int j = 0; j <= this.steps; j++)
{
Vector3 posicion;
// Método builtin en el Vector3 que realiza una interpolación lineal entre dos vectores
// Se «come» el trabajo matemático por nosotros
Vector3.Lerp(ref keyFrames[i].position, ref keyFrames[i + 1].position, (float)j / (float)(this.steps – 1), out posicion);
// Guardamos detalle
detailedInterpolation.Add(new Spline(posicion));
}
}
}
Para debugar bien, dibujaremos los checkpoints en pantalla, eso nos facilitará bastante la vida. El método Draw contiene el siguiente código:
/// <summary>
/// Pinta los keyframes en pantalla (para debug)
/// </summary>
/// <param name=»projection»></param>
/// <param name=»view»></param>
public void Draw(Matrix view, Matrix projection)
{
foreach (Spline spline in keyFrames)
{
spline.Draw(projection, view);
}
}
Como vemos, lo único que hace es recorrer todos los keyframes y dibujarlos por pantlla (pintando un boundingSphere en su lugar). La ejecución dará lugar a nuestro agente recorriendo el circuito, pasando por todos los checkpoints definidos previamente:
Podéis ver un vídeo del resultado de la ejecución del código aquí. El código, como siempre, está disponible para descargar en este enlace.
En un próximo artículo me gustaría hacer que el agente se desplace de una forma menos lineal, haciendo cierta curva entre keyframe y keyframe.

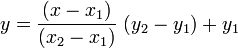


Buen ejemplo, esto se pone aun mas interesante. No habia probado nada de interpolación con XNA, gracias por la intro!!