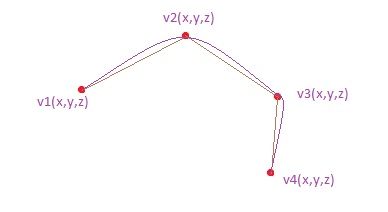
En el post anterior vimos las interpolaciones lineales, una forma muy correcta de desplazar elementos en nuestro «mundo» tridimensional. Lo «malo» de estas, es que la trayectoria entre keyframe y keyframe es una línea recta, y eso hace que estas trayectorias puedan parecer algo «duras» -aunque en ocasiones eso puede ser precisamente lo que estamos buscando-. No obstante, existe una forma más «suave» de desplazamiento. Esto se puede ver claramente con la siguiente representación gráfica:
Nos hemos hecho ya a la idea de que existen distintos tipos de interpolación, vamos a ver ahora la interpolación por medio de spline (a partir de ahora splines…). Los splines se utilizan para aproximar formas complicadas en forma de curvas. Su cálculo es rápido… por lo que son ideales para la programación de juegos. De estos hay tres tipos:
- Splines cúbicos
- Splines Bézier
- B-Splines
Aplicación en XNA
El siguiente código está basado en el fantástico tutorial de Kyle Hayward acerca de interpolacion de movimientos para el desplazamiento de cámaras (que a su vez está parcialmente extraido de una implementación en JAVA).
Respecto el código del ejemplo anterior, deberemos modificar muy poco código, sólo la forma en la que se calcula este tipo de interpolación, así sustituiremos el código del método GenerarInterpolacion() por el siguiente:
// Cada punto de un spline cúbico se ve afectado por cualquier otro punto
// así que será necesario generar las ecuaciones cúbicas para cada punto de control
// teniendo en consideración la curva completa. De eso se encarga el método calculateCubicSpline
Vector3[] positions = new Vector3[this.keyFrames.Count];
for (int i = 0; i < this.keyFrames.Count; i++)
{
positions[i] = this.keyFrames[i].position;
}
Spline[] pos_cubic = calculateCubicSpline(this.keyFrames.Count – 1, positions);
for (int i = 0; i < this.keyFrames.Count – 1; i++)
{
for (int j = 0; j < this.steps; j++)
{
float k = (float)j / (float)(this.steps – 1);
Vector3 center = pos_cubic[i].GetPointOnSpline(k);
detailedInterpolation.Add(new Spline(center));
}
}
La chicha matemática está en el método calculateCubicSpline(), que deberemos añadir a la clase SplinesManager:
/// <summary>
/// Calcula el spline cúbico de los puntos de controls
/// Los segmentos son representados como: a + b*u + c*u^2 + d*u^3
/// Algoritmo obtenido de: http://www.cse.unsw.edu.au/~lambert/splines/
/// </summary>
/// <param name=»n»>el número de puntos de control</param>
/// <param name=»v»>array de vectores</param>
/// <returns></returns>
private Spline[] calculateCubicSpline(int n, Vector3[] v)
{
Vector3[] gamma = new Vector3[n + 1];
Vector3[] delta = new Vector3[n + 1];
Vector3[] D = new Vector3[n + 1];
int i;
/* We need to solve the equation
* taken from: http://mathworld.wolfram.com/CubicSpline.html
[2 1 ] [D[0]] [3(v[1] – v[0]) ]
|1 4 1 | |D[1]| |3(v[2] – v[0]) |
| 1 4 1 | | . | = | . |
| ….. | | . | | . |
| 1 4 1| | . | |3(v[n] – v[n-2])|
[ 1 2] [D[n]] [3(v[n] – v[n-1])]
by converting the matrix to upper triangular.
The D[i] are the derivatives at the control points.
*/
//this builds the coefficients of the left matrix
gamma[0] = Vector3.Zero;
gamma[0].X = 1.0f / 2.0f;
gamma[0].Y = 1.0f / 2.0f;
gamma[0].Z = 1.0f / 2.0f;
for (i = 1; i < n; i++)
{
gamma[i] = Vector3.One / ((4 * Vector3.One) – gamma[i – 1]);
}
gamma[n] = Vector3.One / ((2 * Vector3.One) – gamma[n – 1]);
delta[0] = 3 * (v[1] – v[0]) * gamma[0];
for (i = 1; i < n; i++)
{
delta[i] = (3 * (v[i + 1] – v[i – 1]) – delta[i – 1]) * gamma[i];
}
delta[n] = (3 * (v[n] – v[n – 1]) – delta[n – 1]) * gamma[n];
D[n] = delta[n];
for (i = n – 1; i >= 0; i–)
{
D[i] = delta[i] – gamma[i] * D[i + 1];
}
// now compute the coefficients of the cubics
Spline[] C = new Spline[n];
for (i = 0; i < n; i++)
{
C[i] = new Spline(v[i], D[i], 3 * (v[i + 1] – v[i]) – 2 * D[i] – D[i + 1],
2 * (v[i] – v[i + 1]) + D[i] + D[i + 1]);
}
return C;
}
Si ejecutamos este código, el resultado va a ser que ahora el agente se mueve por el circuito tomando las curvas suavemente.
[View:http://www.youtube.com/watch?v=jLqfB6W0WDg:550:0]