¡Hola a todos!!
Como lo prometido es deuda, hoy vamos a hacer una pequeña introducción al algoritmo de aprendizaje del perceptrón binario, el cual es bastante utilizado en Machine Learning en clasificación supervisada.
Como ya sabréis, este tipo de clasificación es aquella en la que inicialmente tenemos un conocimiento acerca de la categoría o clase al que pertenecen cada uno de los elementos del conjunto de datos de entrenamiento.
Ej: Sentimiento de un tweet -> Positivo o negativo.
| Contenido Tweet | Positivo/Negativo |
| Gracias por el vídeo, sería muy bueno conocer también la configuración de tu terminal, esta genial. Saludos. | Positivo |
| ¡No estoy nada de acuerdo con lo que acabas de escribir, es indignante!
|
Negativo |
| Me he enterado tarde del evento 🙁 Supongo que habrá que esperar al año que viene
|
Negativo |
Perceptrón Binario
Durante muchos años, el campo de la Inteligencia Artificial ha intentado imitar al ser humano, y el algoritmo del perceptrón no iba a ser menos.
El modelo biológico más simple de un perceptrón es una neurona:
- La neurona es una célula especializada y caracterizada por poseer una cantidad indefinida de canales de entrada llamados dendritas y un canal de salida llamado axón.
- Las dendritas operan como sensores que recogen información de la región donde se hallan y la derivan hacia el cuerpo de la neurona que reacciona mediante una sinapsis enviando una respuesta hacia el cerebro.
Una posible representación de un perceptrón con 5 señales de entrada podría ser la siguiente:
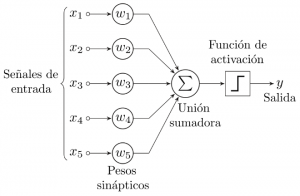
Si comparamos la imagen anterior con una neurona:
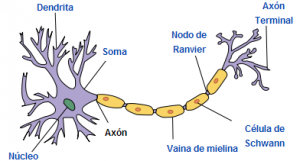
Las señales de entrada son captadas por las dendritas. La función de activación sería el proceso de sinapsis que se realiza dentro de la neurona, y la salida producida se conduciría a través del axón hasta llegar al axón terminal.
Pero ¿Cómo representamos esto matemáticamente? Al final nuestro ordenador sólo entiende de estas cosas…
![]()
Pues bien, podemos definirnos una función como la anterior donde “w” es nuestro vector de pesos y “x” es un vector con los valores de las características de lo que queremos predecir. El operador “·” representa la operación algebraica del producto escalar y “b” representa el concepto de bias (el cual explicaremos más adelante).
Al fin y al cabo, nuestro modelo define un hiperplano en un espacio n+1 dimensional.
![]()
En el caso de un espacio de dos dimensiones:
![]()
Esta es una ecuación lineal, donde “m” representa la pendiente y “b” determina el punto donde la recta corta al eje Y.
![]()
Si representamos nuestro conjunto de datos en dos dimensiones, obtendríamos la siguiente gráfica:
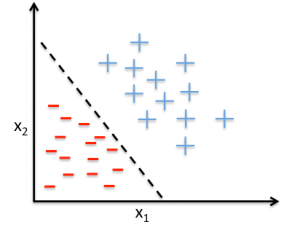
Donde a un lado de la línea (por ejemplo) estarían los datos que pertenecen a un tweet positivo y al otro lado los que pertenecen a tweets negativos.
En resumen, podemos decir que la función definida anteriormente se usará para clasificar “x” como un tipo u otro. Hasta aquí todo parece bastante claro… pero… ¿Cómo calculamos nuestro vector de pesos?
Esta fase en la que calculamos el vector de pesos se denomina “entrenamiento”. Siempre que hablamos de aprendizaje supervisado vamos a tener dos fases principalmente:
- Entrenamiento: Cogemos un subconjunto de datos de nuestro dataset con el que vamos a entrenar nuestro modelo para que “aprenda a predecir”.
- Test: En esta fase cogemos el subconjunto de datos restante de nuestro dataset y comprobamos que nuestro modelo entrenado anteriormente es capaz de predecir correctamente observaciones nuevas que no hayan aparecido en el conjunto de datos de entrenamiento.
A continuación, vamos a describir cómo se entrenaría nuestro perceptrón y cómo se van ajustando los pesos:
Imaginemos un conjunto de datos que vamos a utilizar en nuestro periodo de aprendizaje.
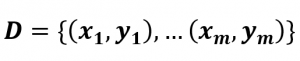
Cada “x” es una característica de nuestro dato e “y” es el valor esperado.
Para cada pareja (x,y) del conjunto de datos anterior aplicamos la siguiente regla de actualización de pesos:
![]()
- α es la tasa de aprendizaje (número entre 1 y 0).
- δ es la salida de la neurona.
Veamos un ejemplo:
Considerando que bias es 0 y la tasa de aprendizaje 0.1.
| Entrada | Pesos | Salida | Error | Corrección | Pesos finales | |||||
| x0 | x1 | y | wo | w1 | dot | δ | y -δ | α (y – δ) | wo | w1 |
| 4.8 | 1.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4.6 | 1.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 4.5 | 1 | 0 | 0 | 0 | 0 | 1 | 0.1 | 0.6 | 0.45 |
| 4.6 | 1.4 | 0 | 0.6 | 0.45 | 3.39 | 1 | -1 | -0.1 | 0.14 | 0.31 |
| 5.6 | 3.6 | 1 | 0.14 | 0.31 | 1.9 | 1 | 0 | 0 | 0.14 | 0.31 |
| 5.5 | 1.3 | 0 | 0.14 | 0.31 | 1.17 | 1 | -1 | -0.1 | -0.41 | 0.18 |
Algoritmo
A continuación, se muestra una implementación del perceptrón binario en Python.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Perceptron(object): """Binary Perceptron""" def __init__(self, eta=0.1, bias=0): self.eta = eta self.bias = bias self.weights = None self.errors = 0 def fit(self, x, y): """Fit perceptron""" x_values = x.values if isinstance(x, pd.DataFrame) else x y_values = y.values if isinstance(y, pd.DataFrame) else y self.weights = np.zeros(x.shape[1], dtype='float') for index_x, target in zip(x_values, y_values): update = self.eta * (target - self.predict(index_x)) self.weights += update * index_x self.errors += int(update != 0.0) return self def __net_input(self, x): return np.dot(x, self.weights) + self.bias def predict(self, x): """Predict perceptron""" return np.where(self.__net_input(x) > 0, 1, 0) |
Hemos creado una pequeña clase que tiene como principales métodos:
- Fit: Para entrenar nuestro modelo con los datos existentes.
- Predict: Método que predecirá la clase a la que corresponde cada uno de los elementos del dataset que se proporcionen.
Además, el constructor de la clase puede recibir dos parámetros: learning rate y bias (del que hablaremos al final del artículo), para que puedan ser ajustados en función de nuestras necesidades. En este caso, el learning rate suele ser un valor entre 1 y 0. Determina como de rápido son ajustados los pesos, si aumentamos este parámetro podemos hacer que nuestro algoritmo converja más rápido, pero cuidado, podríamos pasarnos y hacer que no se converja correctamente. Por otro lado, si este valor es muy pequeño, nuestro algoritmo puede tardar más en converger, incrementando el tiempo de entrenamiento.
Ejemplo
Todo esto está muy bien, pero… vamos a probarlo con un ejemplo real para ver si nuestro algoritmo funciona correctamente, y lo más importante, saber si nuestro modelo es bastante bueno prediciendo.
Planta Iris
¿Sabéis que existe un tipo de planta que se llama Iris? Yo la conocí hace ya bastantes años, cuando hice mi primer proyecto con Machine Learning. Este dataset de los años 30 es empleado con frecuencia como ejemplo en la mayoría de cursos y libros que tratan sobre este tema. De cada planta de la especie Iris (Setosa, Versicolor y Virgínica) se han tomado medidas de longitud y ancho de sépalo y pétalo (cm), por lo que nuestro dataset tiene 4 características y una columna extra que nos informa del tipo de Planta. En total, este conjunto de datos cuenta con 150 Plantas (50 de cada tipo).
Podéis decargaros el dataset en la siguiente url : https://archive.ics.uci.edu/ml/datasets/iris

Como el perceptrón que hemos desarrollado solo es apto para problemas de clasificación binaria, vamos a eliminar del conjunto de datos las plantas de tipo Virgínica.
Antes de empezar a entrenar el modelo vamos a representar los datos que tenemos actualmente en el dataset.
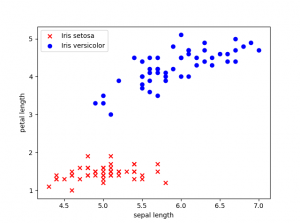
Nuestro dataset tiene cuatro características, pero para poder representarlo en dos dimensiones hemos escogido la longitud en cm del pétalo y del sépalo.
Entrenamiento
Para entrenar nuestro modelo vamos a dividir nuestro dataset en dos, uno para test y otro para entrenamiento, en este caso hemos reservado un 50% para test y un 50% entrenamiento. Es importante que la separación que hagáis sea aleatoria, porque si la hacemos secuencial puede que la mayoría de datos que vayan a entrenamiento sean solamente de una clase, y luego nuestro modelo no prediga correctamente porque no se entrenó con una mínima variedad de todas las clases y ejemplos.
|
1 2 3 4 5 |
train, test = train_test_split(dataframe, test_size=0.5, random_state=42) perceptron = Perceptron() x_train = train.loc[:, ['sepallength', 'petallength']] y_train = train.loc[:, 'class'] perceptron.fit(x_train, y_train) |
Test
Una vez que hemos entrenado nuestro modelo, podemos llamar a la función predict de nuestra clase perceptrón para que realice las predicciones sobre los datos que hemos reservado para test.
|
1 2 |
classification = perceptron.predict(test.loc[:, ['sepallength', 'petallength']]) test = test.assign(irisclassification=classification) |
La función predict devuelve las clases que se han predicho para cada una de las plantas de nuestro dataset.
Decision boundary
El límite de decisión define una línea sobre el espacio de entrada, en un lado de la línea la salida de nuestro perceptron sería de tipo 0 y en el otro lado de tipo 1.
Para poder pintar esta línea veréis bastantes ejemplos en los que utilizan el contorno; calculan todos los puntos del plano y vuelven a predecir el valor para cada uno de los resultados.
Este proceso me parece demasiado complejo para lo que se quiere representar de manera gráfica.
Como hemos entrenado nuestro modelo con dos características, nuestra línea de decisión viene determinada por:
![]()
Donde b es bias.
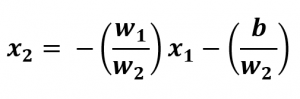
El rango de valores para X1 irá desde el mínimo de la longitud de sépalo hasta el máximo de nuestro conjunto de datos.
Sin tener en cuenta en este caso bias, podríamos pintar nuestra línea de decisión teniendo en cuento los cálculos anteriores:
|
1 2 3 4 5 6 7 |
def plot_decision_boundary(x1, model): x_min, x_max = x1.min() - 1, x1.max() + 1 weights = -model.weights[0] / model.weights[1] line_points = np.linspace(x_min, x_max) plt.plot(line_points, weights * line_points - (model.bias / model.weights[1])) |
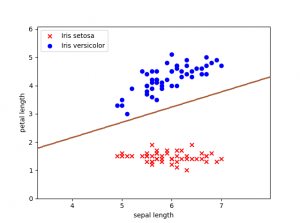
Ahora que se ha mencionado de nuevo el término de bias, creo que va siendo hora de explicar que es lo que representa. Si habéis leído anteriormente algo sobre el tema en varios artículos también lo denominan sesgo. Este valor va a permitir cambiar la función de activación de nuestro perceptrón de izquierda a derecha, otorgándole más flexibilidad para aprender. Espacialmente hablando vamos a poder mover cada punto de la línea de decisión a una distancia constante y en una dirección específica. Si entrenamos nuestro perceptrón con un valor de bias=1, podemos ver cómo afecta a la línea de decisión.
Nuestra línea se situará más cerca del conjunto de datos que representan las plantas Iris de tipo Setosa.
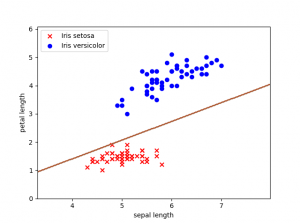
Limitaciones
Anteriormente hemos representado nuestros datos en 2 dimensiones, y se aprecia que los dos tipos de plantas Iris setosa e Iris versicolor son linealmente separables. Podemos encontrar distintas líneas que separen nuestro conjunto de datos en el espacio.
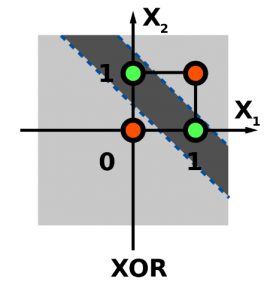
Una de las principales y más importantes limitaciones que tiene el perceptrón es que, si los datos no son linealmente separables, la línea del algoritmo no se garantiza que converja. Por ejemplo, nuestro perceptrón binario nunca podría aprender correctamente la función de XOR, ya que requiere al menos dos líneas para separar las clases (0,1).
Espero que os haya gustado esta primera introducción al perceptrón binario.
Os dejo todo el código de python que he utilizado en un repositorio de mi github. Por si queréis cambiar parámetros o realizar una ejecución más rápida, he subido el código a un Notebook de IPython situado en Azure Notebooks.
¡Nos vemos en el siguiente post!

Deja un comentario